Research💡

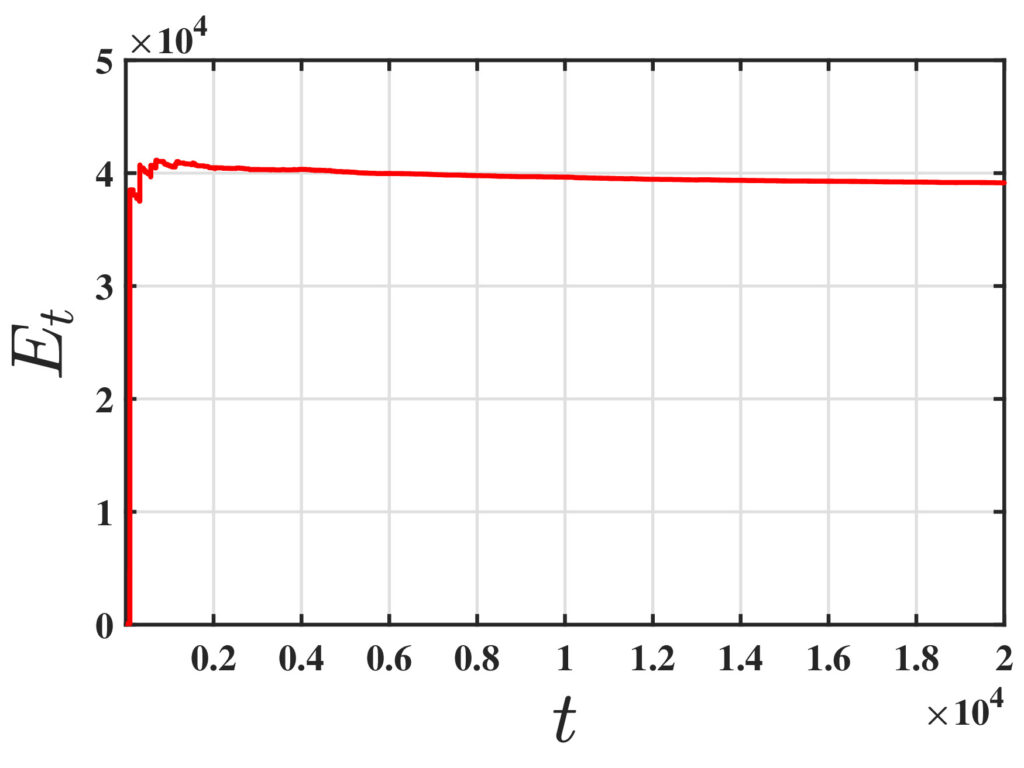
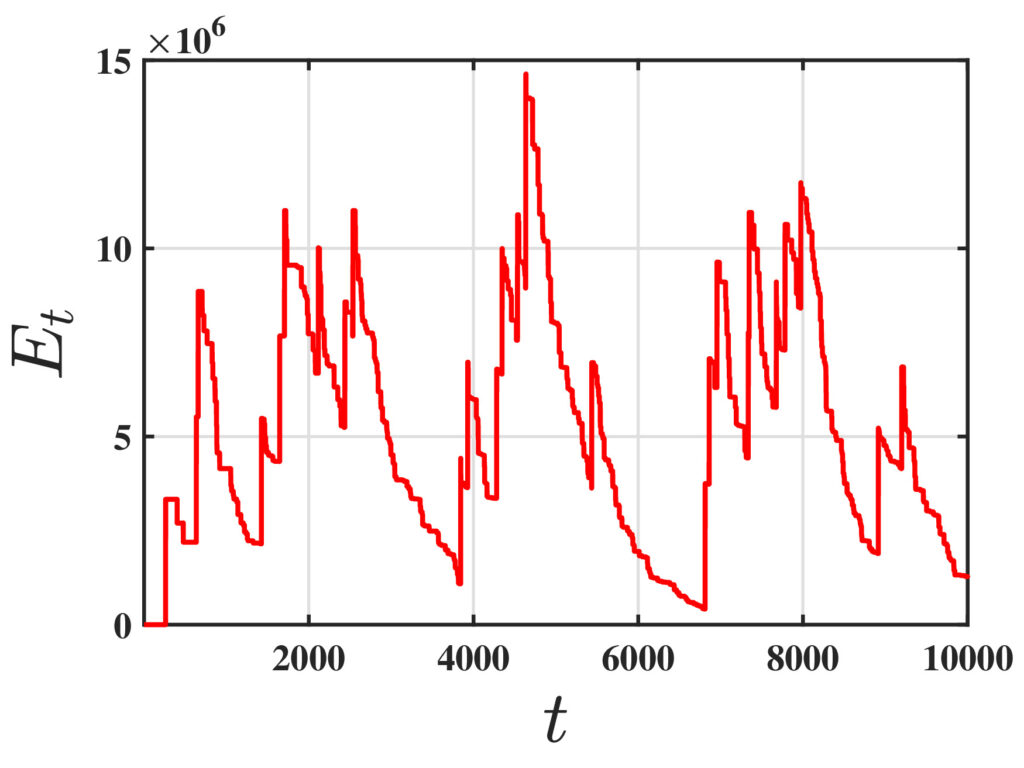
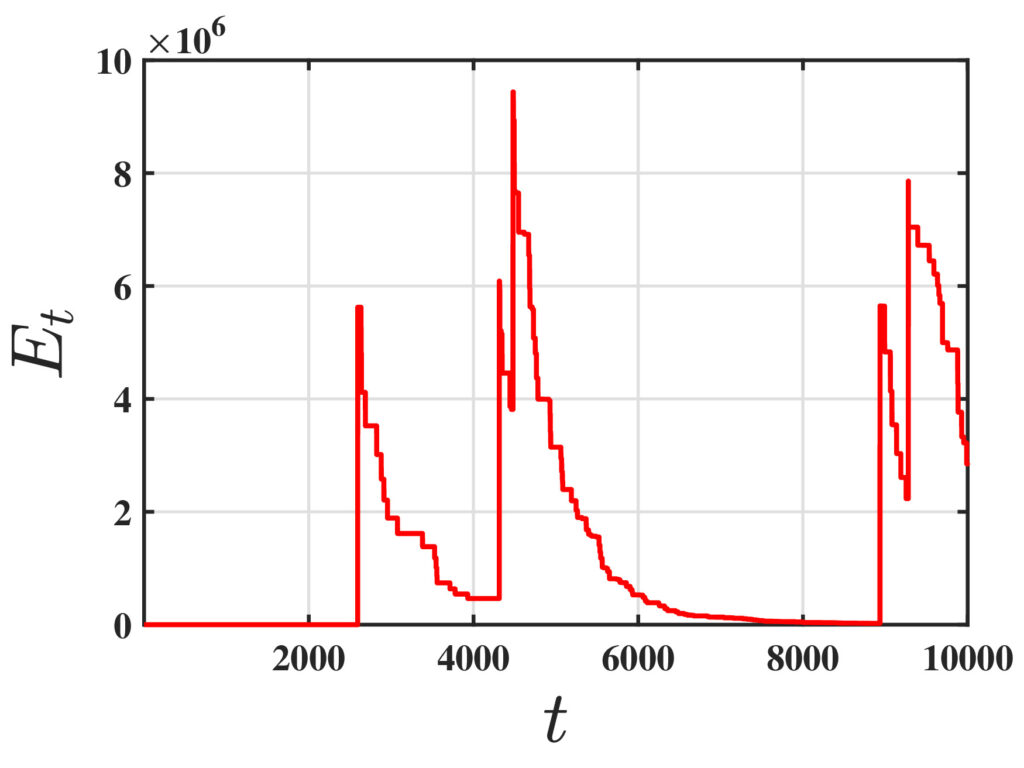
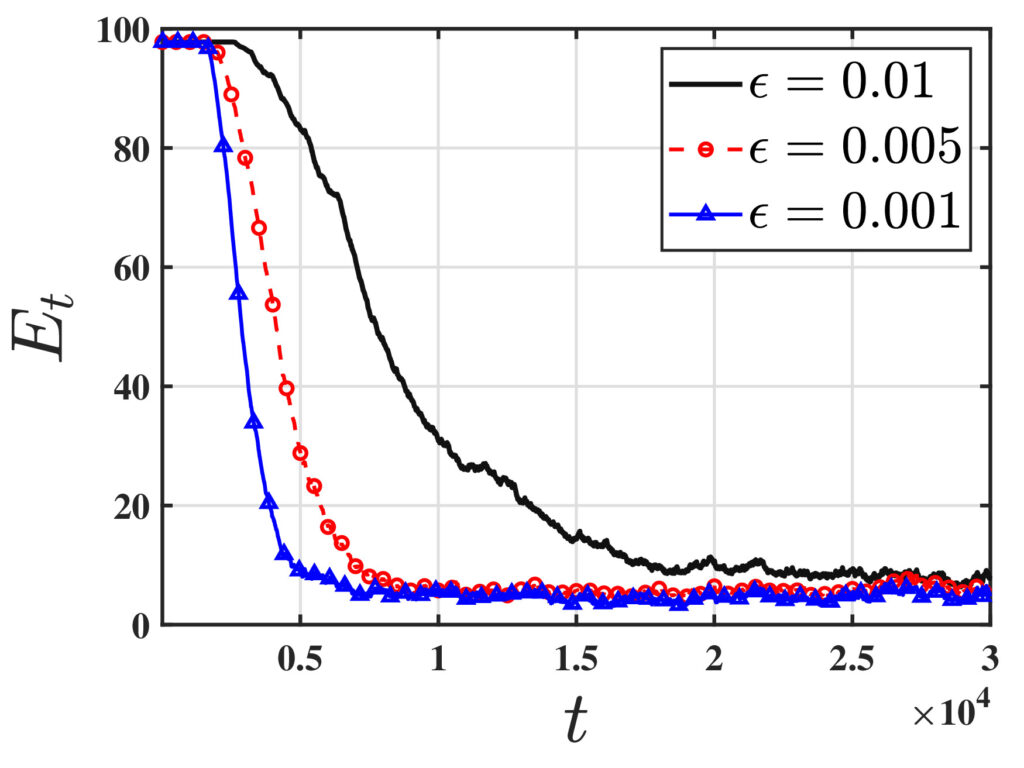
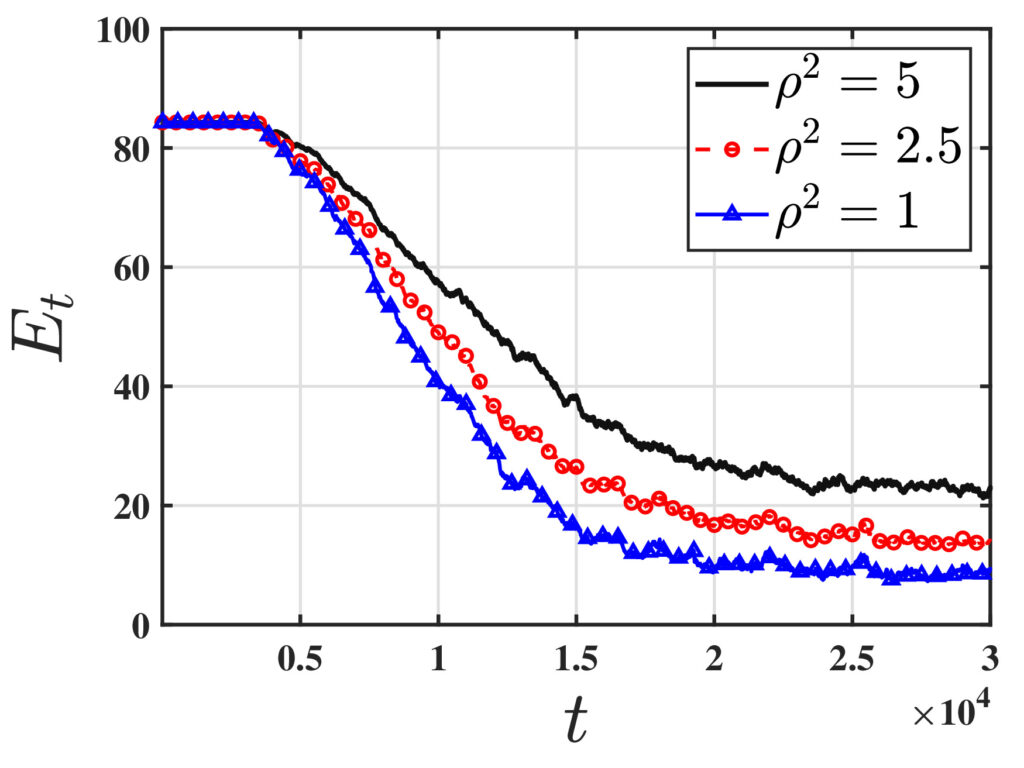
One of the fundamental challenges in reinforcement learning (RL) is policy evaluation, which involves estimating the value function—the long-term return—associated with a fixed policy. The well-known Temporal Difference (TD) learning algorithm addresses this problem, and recent research has provided finite-time convergence guarantees for TD and its variants. However, these guarantees typically rely on the assumption that reward observations are generated from a well-behaved (e.g., sub-Gaussian) true reward distribution. Recognizing that such assumptions may not hold in harsh, real-world environments, we revisit the policy evaluation problem through the lens of adversarial robustness.

To the best of our knowledge, these results are the first to examine adversarial robustness in stochastic approximation schemes driven by Markov noise. A key technical innovation underlying our results is the analysis of the Median-of-Means estimator in the context of corrupted, time-correlated data, which may also be of independent interest to the field of robust statistics.

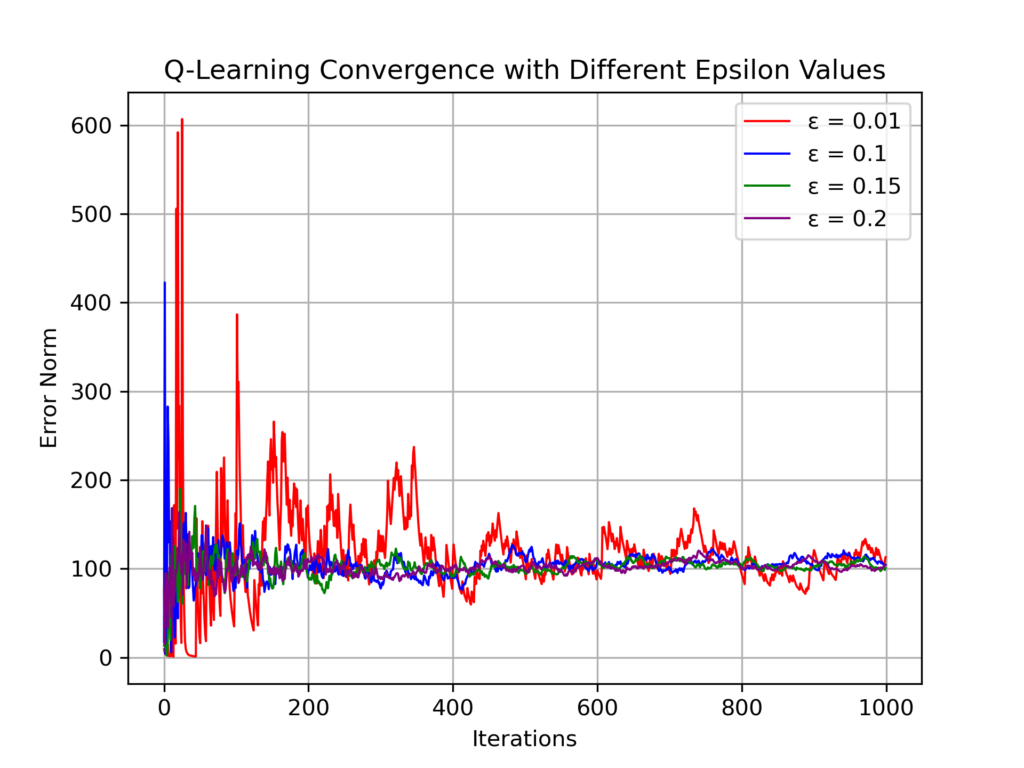
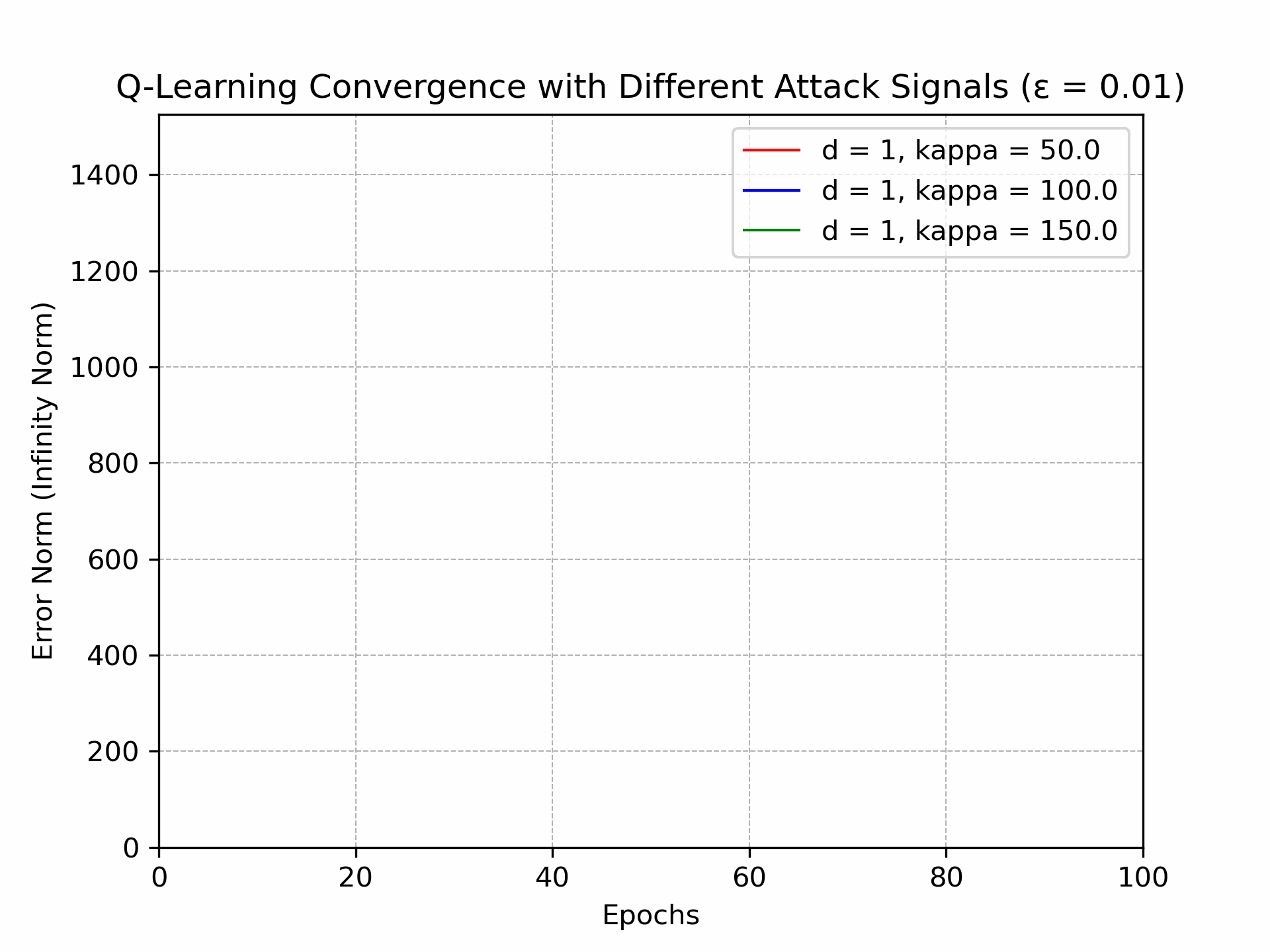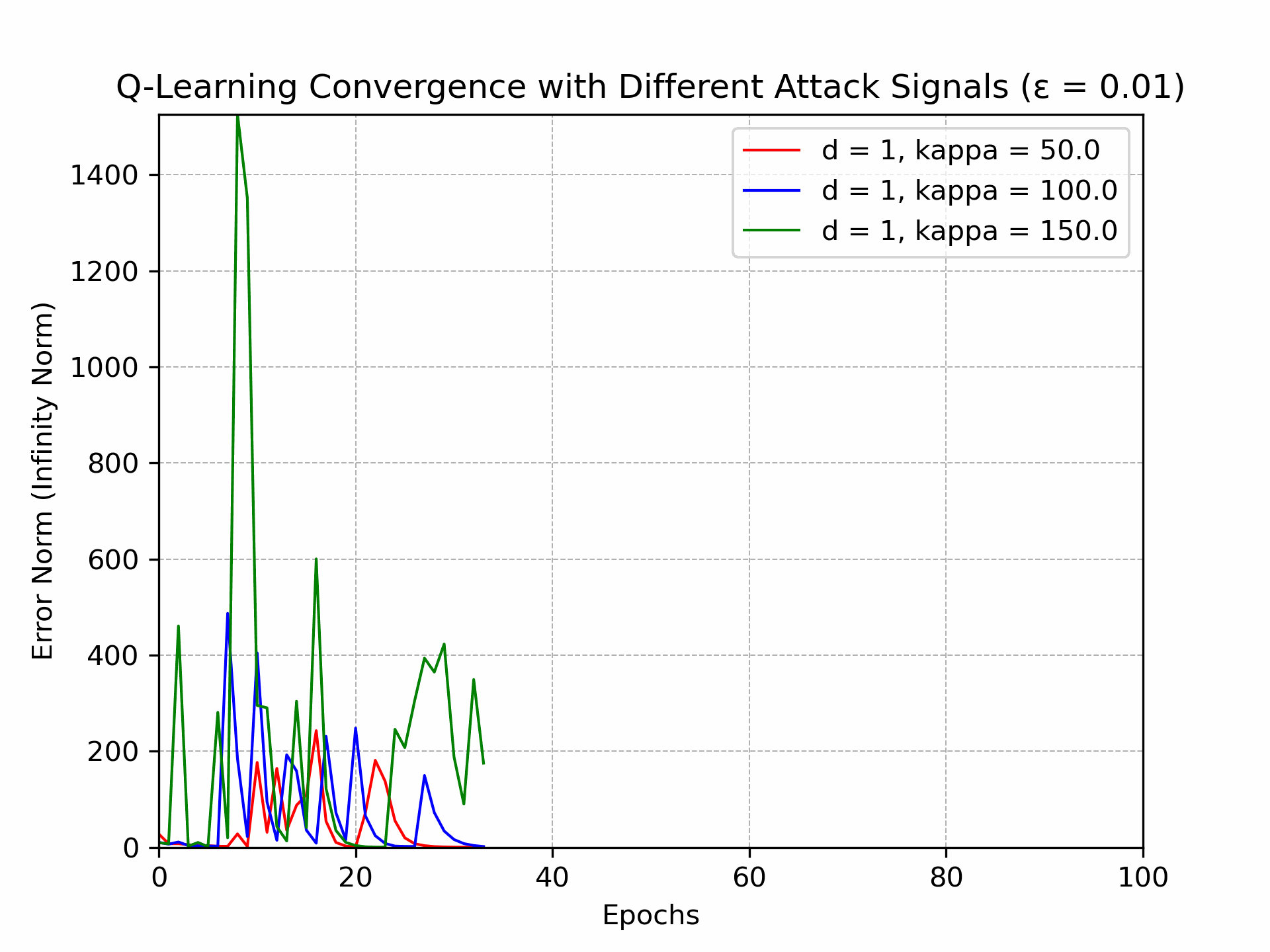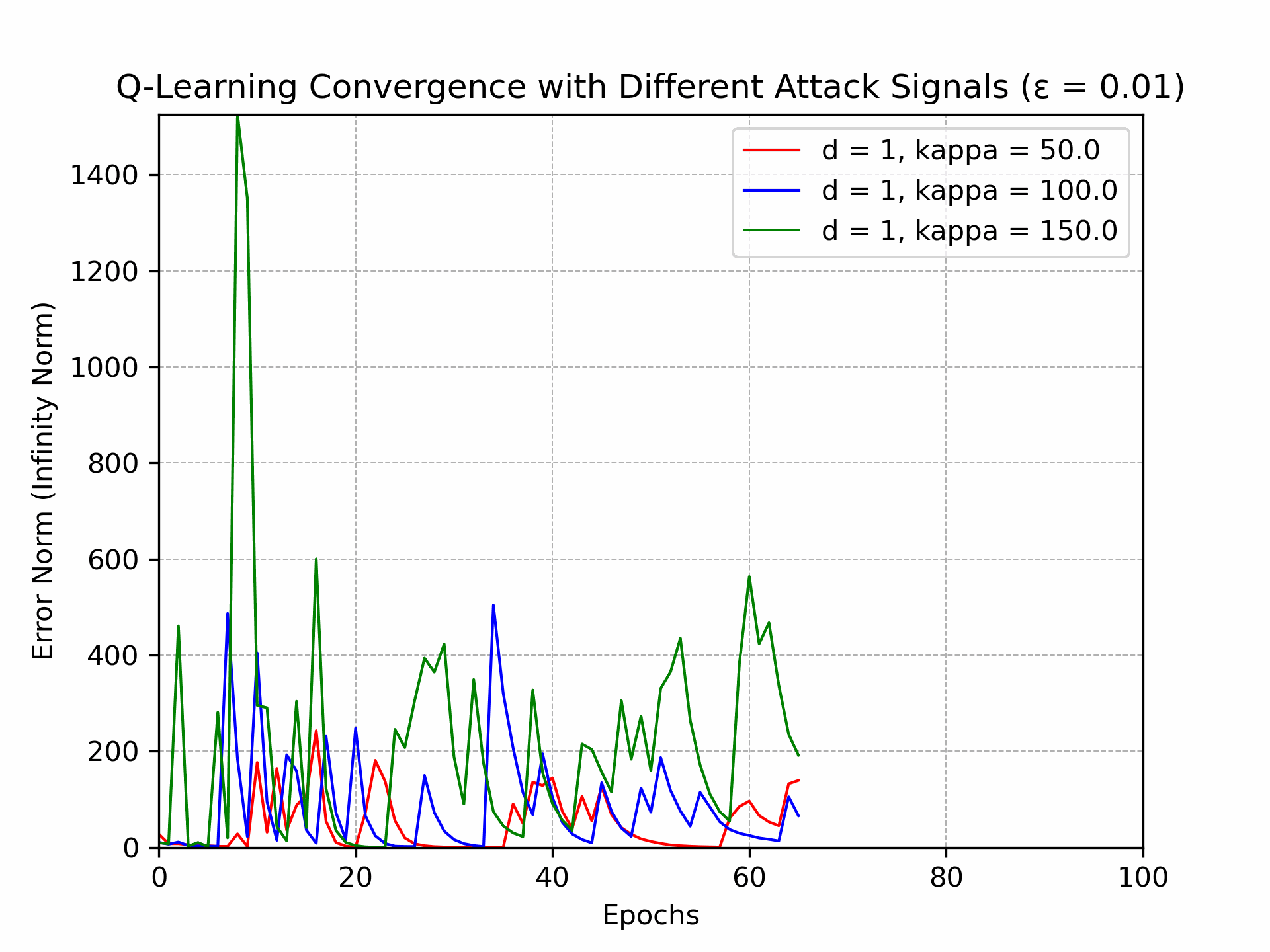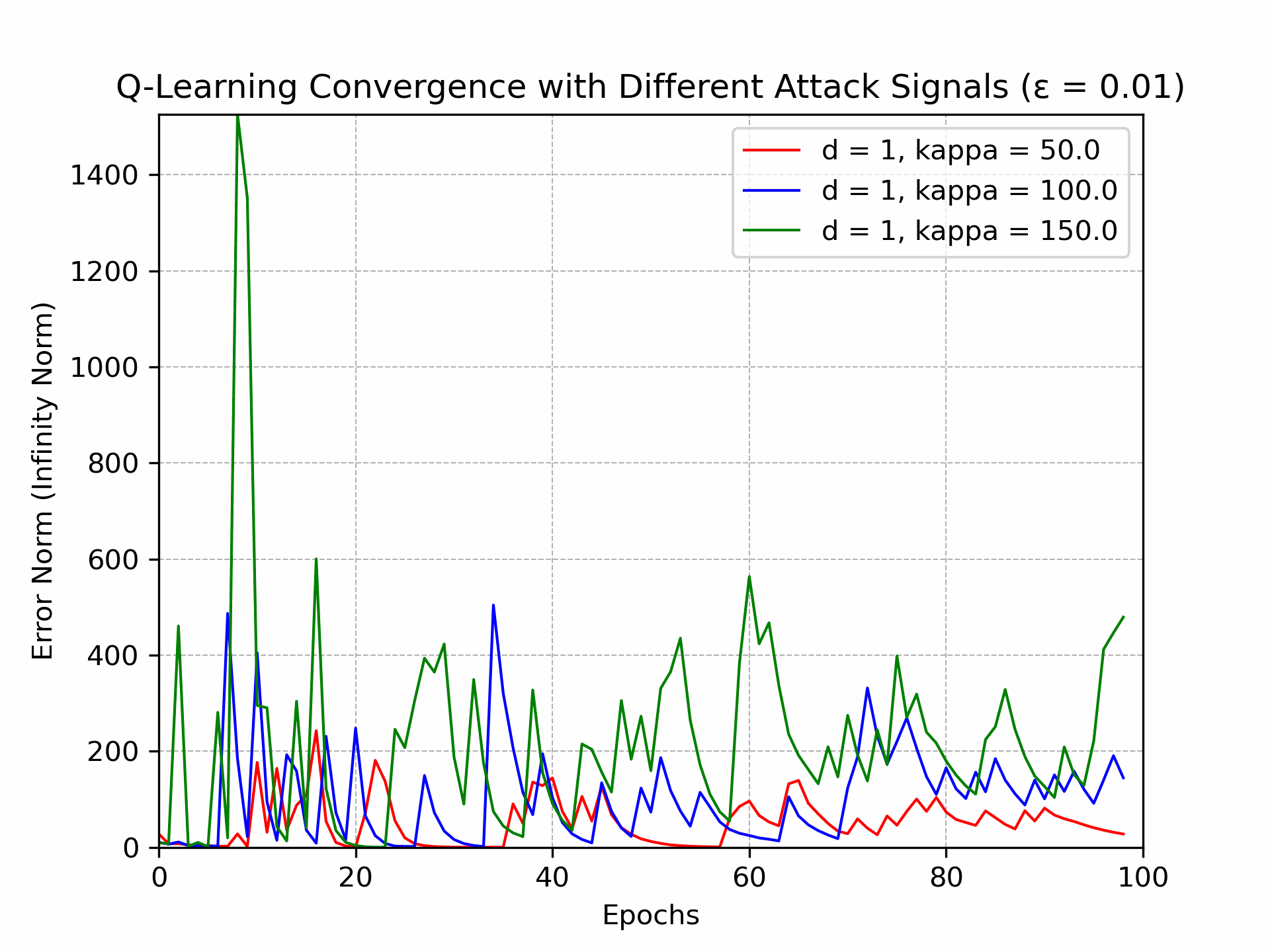
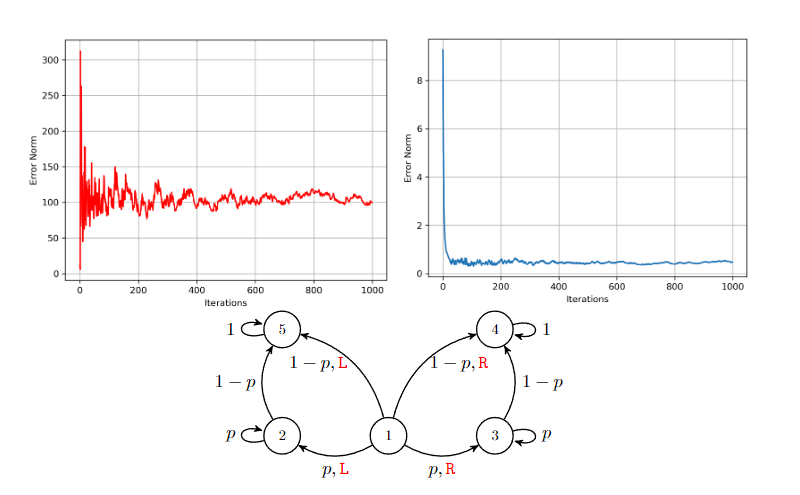
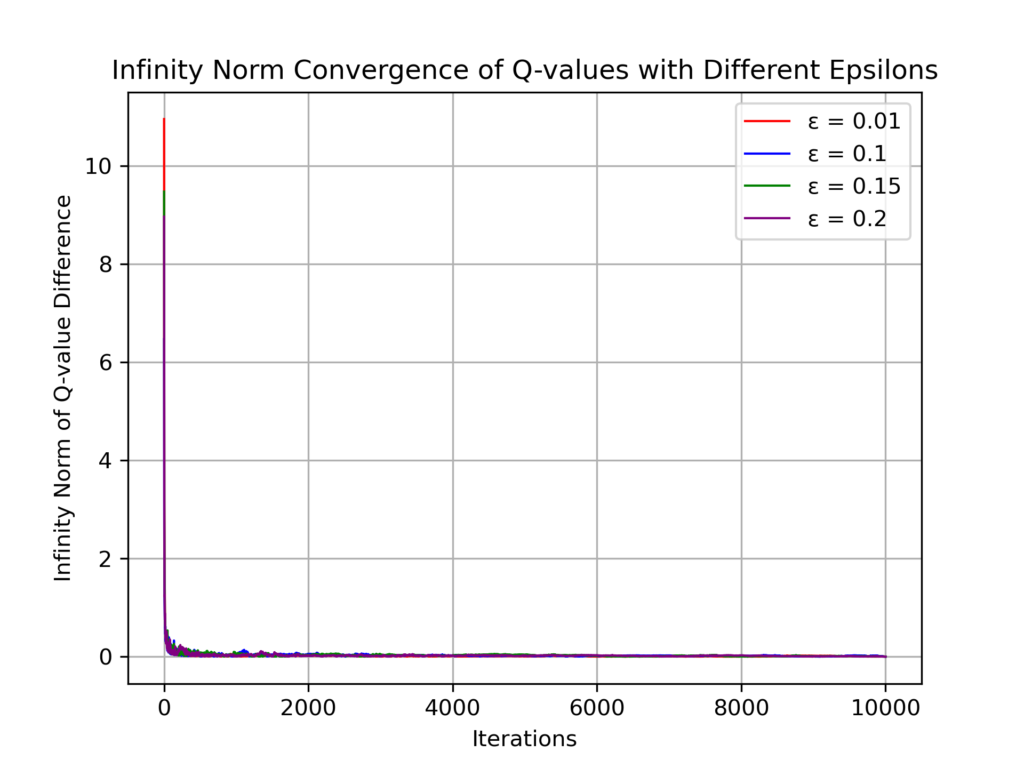
Recently, there has been a surge of interest in analyzing the non-asymptotic behavior of model-free reinforcement learning algorithms. However, the performance of such algorithms in non-ideal environments, such as in the presence of corrupted rewards, is poorly understood. Motivated by this gap, we investigate the robustness of the celebrated Q-learning algorithm to a strong-contamination attack model, where an adversary can arbitrarily perturb a small fraction of the observed rewards. We start by proving that such an attack can cause the vanilla Q-learning algorithm to incur arbitrarily large errors. We then develop a novel robust synchronous Q-learning algorithm that uses historical reward data to construct robust empirical Bellman operators at each time step. Finally, we prove a finite-time convergence rate for our algorithm that matches known state-of-the-art bounds (in the absence of attacks) up to a small inevitable error term that scales with the adversarial corruption fraction. Notably, our results continue to hold even when the true reward distributions have infinite support, provided they admit bounded second moments. This work has been accepted for presentation, and publication in the proceedings of 63rd IEEE Conference on Decision and Control, 2024!